11
P = P
1
+ P
2
+ P
3
…….. P
n
r
When P = Average annual rainfall, r = no. of rain gauge stations
P
1
, P
2
, P
3
…. P
n
= Rain fall in different rain gauge stations
This number is more or less satisfactory when the density of rain gauges are
high and the rain fall variations from station to station is not high. This method,
however, has serious drawback as it does not take into account the weightage
of area of different rain gauge stations.
(2)
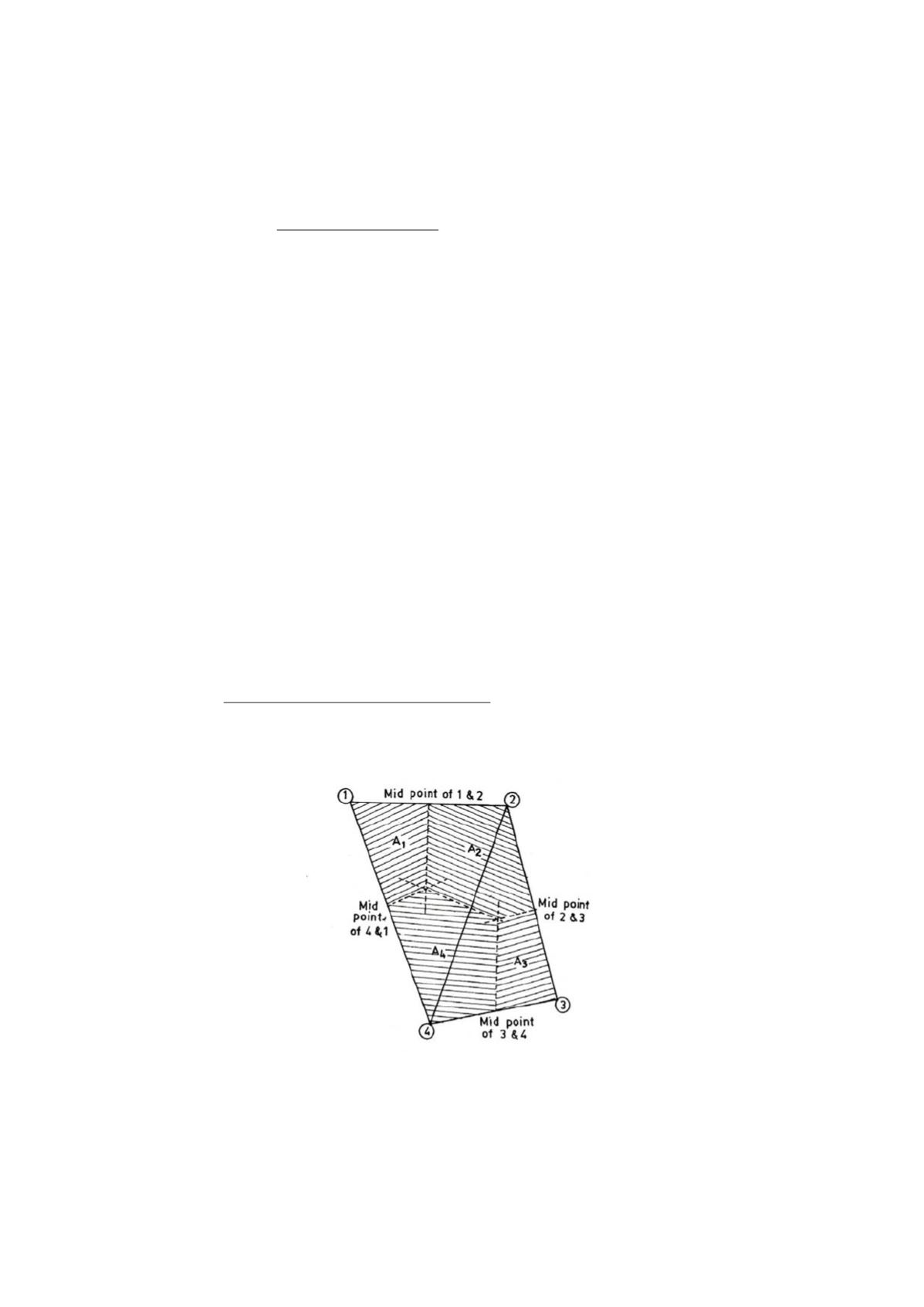
Thiessen's Polygon method
This method (Fig. 1.3) takes into account the weightage of area of influence of
each rain gauge stations. Adjacent stations are joined by straight lines, thus
dividing the entire area into a series of triangles. Perpendicular bisectors are
erected on each of these lines, thus forming a series of polygons, each
containing one and only one rainfall station. The rainfall recorded at a station is
assigned the value to the polygon within which the station is located. Thus, if P
is the mean rainfall of the basin of area A, then
P = A
1
P
1
+ A
2
P
2
+ A
3
P
3
------ A
n
P
n
A
When P
1
, P
2
, P
3
etc. represents rainfalls at the respective stations,
whose surrounding polygons have the areas A
1
, A
2
, A
3
etc.
Fig. 1.3 : Theissen's Polygon Method (After Punnia et al, 1992)


